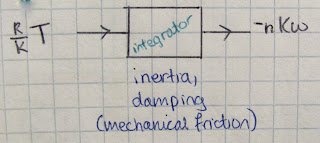
We abstract the circuit from the previous image to become this:
Next, Oscar explained more information about our system that we can derive by knowing torque.:
Torque proportional to angular speed is friction.
An object exposed to friction slows down.
Torque proportional to angular position is a "spring."
The greater the angular position of the pendulum, the greater the torque causing it to swing back.
Next Oscar introduced us to two important formulas:
The rate of change of position is angular speed.
The rate of change of speed is acceleration.
We want torque proportional to position such that we make a spring. But how do we go from speed to position? (ω → θ) We integrate it. A capacitor integrates current to produce a change in voltage. (flashback to calculus 101: the integral of speed is position).
Then Oscar showed us this circuit....
... and explained this abstraction:
After all that, it was time to get to the breadboards. We started by creating this:
The effect of the virtual spring created this on the oscilloscope:
We had fun with the settings, and were able to have the oscilloscope measure the output like this (looks like a galaxy, no?):
Using Legos, we created a pendulum that demonstrates the properties of a spring:














No comments:
Post a Comment